Written by Akshay Jaggi
on May 02, 2016

Suffix Automata

Abstract

I found out about Suffix Automata (SA) while reading accepted solutions of a problem we were unable to solve in one of the Codeforces-GYM practice sessions. Most of the solutions were using Suffix Arrays, but this particular solution. It was neat, short and precise. I started looking up more on Suffix Automata. It has been used mostly by Russian coders, and the only available and highly quoted resource I found is in Russian. It took me about a week on the Yandex translated resource, and countless re-reads before I was finally able to make sense of what was written.

Suffix Automata is one of the few very elegant data structures I know of. Coarsely, you can consider it as a data structure which contains information about all the substrings of a given string. You can solve a wide range of problems using it and it is linear in memory and construction time. For example, from the definition, you know you can solve the trivial problem of checking if the given strings occur as a substring of a given text, in linear time.

This blog post is long overdue now. I have been waiting to write this for three months.

Definition

A suffix automaton, also known as Directed-Acyclic-Word-Graph (DAWG), for a string S is the minimal deterministic finite automaton (DFA) that accepts all suffixes of the given string S.

Observation 1: If you mark all the states of the DFA as accepting, you can match any substring of the given string S.

Observation 2: If you want to match the empty string ε, mark the initial state as accepting, otherwise, mark it as non-accepting.

Note 1: If you don’t know what a DFA or an NFA is, I would recommend that you stop reading now and take up a course on Formal Methods. Although describing it here would help with the description of SA, I’m not doing it for the purposes of brevity and clarity.

Note 2: The minimality condition is a very important property, as we will see ahead.

Note 3: I’m using the usual definition of a DFA where DFA is a five-tuple (Q, Σ, δ, q₀, F). Therefore, the initial state will be shown as q₀, etc.

Examples

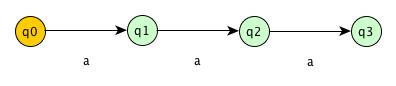
Suffix Automata for S = “aaa”

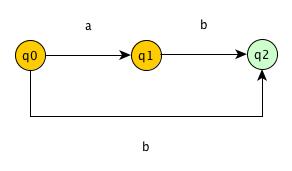Suffix Automata for S = “aaa”

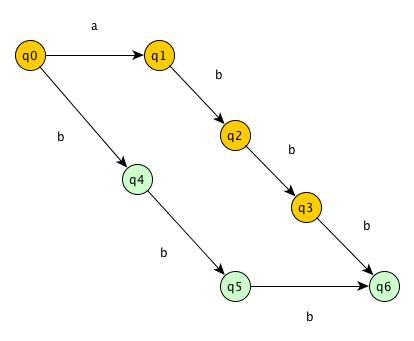Suffix Automata for S = "ab" Suffix Automata for S = “ab” Suffix Automata for S = "abbb" Suffix Automata for S = “abbb” # More Definitions and Properties

Endpos

Let t be a substring of string S. Then, endpos(t) is defined as:

endpos(t): The set of all positions in the string S where the substring t ends.

For example, let

S = "abcdbc"

then,

endpos("bc") = {3,6}
endpos("abc") = {3}

Endpos-Equivalence

Two substrings, t1 and t2, are endpos-equivalent if and only if

 endpos(t1) = endpos(t2)

For example, in the previous string S,

endpos("c") = endpos("bc") = {3,6}
endpos("bc") != endpos("abc")

Thus, “bc” and “c” are endpos equivalent, but “bc” and “abc” are not.

Observation 3: We can divide the set of all non-empty substrings of String S into different endpos-equivalence classes.

Axiom 1: For each endpos-equivalence class, we have a state in the Suffix Automata. All substrings belonging to a given equivalence class, end at the state defined by that equivalence class (when matched by the DFA).

For now just take it as an axiom and remember it by heart. (I’m still figuring out a way to say this better.)
This is the most important part and this is the part where, I believe, the actual beauty of the SA construction lies. As you will see ahead, SA construction involves two different data structures, which individually look quite independent, but they help in building each other incrementally. This is the part that links both the data structures.

Lemma 1: Two non-empty substrings t1 and t2, with length(t1) <= length(t2), are endpos-equivalent if and only if t1 occurs in S only as a suffix of t2.

Proof: This is simple to see. If the ending positions of substrings t1 and t2 are the same, and length(t1) <= length(t2), then t1 can only occur as a suffix of t2. Other way around, if t1 only occurs in S as a suffix of t2, ending positions of t1 would be the same as ending positions of t2.

Lemma 2: Given two non-empty substrings t1 and t2, with length(t1) <= length(t2), then

endpos(t2) ⊆ endpos(t1)       ... if t1 is a suffix of t2
endpos(t1) ∩ endpos(t2) = φ   ... otherwise

Proof: Suppose endpos(t1) and endpos(t2) have at least one element common, say z. This means that they both end at z. And since, length(t1) <= length(t2), therefore t1 is a suffix of t2. Now, since t1 is a suffix of t2, t1 ends at all the places where t2 ends, and maybe a few more places. Therefore, endpos(t2) ⊆ endpos(t1).

Lemma 3: Suppose the length of the minimum length substring in a given equivalence class is a and the length of the maximum length substring is b. Then,

The equivalence class contains one and only one substring for each of the lengths in the range [a,b].
Every substring, say t, in the equivalence class is a proper suffix of all the other substrings in the equivalence class with length greater than length(t).

For example,

{"abcd", "bcd", "cd"} is a valid equivalence class.
{"abcd", "cd"} is not a valid equivalence class.
{"abcd", "cd", "bd"} is not a valid equivalence class.

Proof: Let Q be some endpos equivalence class with more than one string (the proof is trivial for those with one string). From lemma 1, we have that two different strings are endpos-equivalent if and only if one is a proper suffix of the other. Therefore, two different strings of the same length cannot be in an equivalence class.

Now, we need to show that there is one string for each of the lengths between a and b, in Q. Let c be such that a <= c <= b. Let ω be the string of length b in Q**. Therefore, from lemma 2, we have

endpos(ω) ⊆ endpos(suffix of ω of length c) ⊆ endpos(suffix of ω of length a)

But, we already know that

endpos(ω) = endpos(suffix of ω of length a)

as both belong in the same equivalence class Q.

Therefore,

endpos(ω) = endpos(suffix of ω of length c) = endpos(suffix of ω of length a)

Suffix Link Tree

Suffix Link Tree is the second data structure I was talking about.

Suffix Link

Let’s take an equivalence class Q. Let ω be the longest string in this equivalence class, and let this equivalence class cover a range of lengths [a,b]. Therefore, length( ω ) = b and all suffixes of ω of length from a to b-1 are also part of this equivalence class.

But what about the suffix of length a-1 of ω ? It lies in a different equivalence class. Suffix Link links these two equivalence classes.

More precisely, link(Q) points to the endpos-equivalence class
defined by "the longest suffix of w which does not belong to Q".

Observation 4: The suffix links form a tree, with the root as q₀ (the initial state of the suffix automata).

The root is the equivalence class defined by the empty string.

endpos(“”) = { 0, 1, 2, … , strlen(S) }

For any given state, as we travel along the suffix links, we keep on reducing the string length, finally reaching the root node. Lastly, there are no cycles, as only one suffix link exists for any node (parent pointers).

Let’s see the suffix automata and the suffix link tree for S = “abcdbc”.

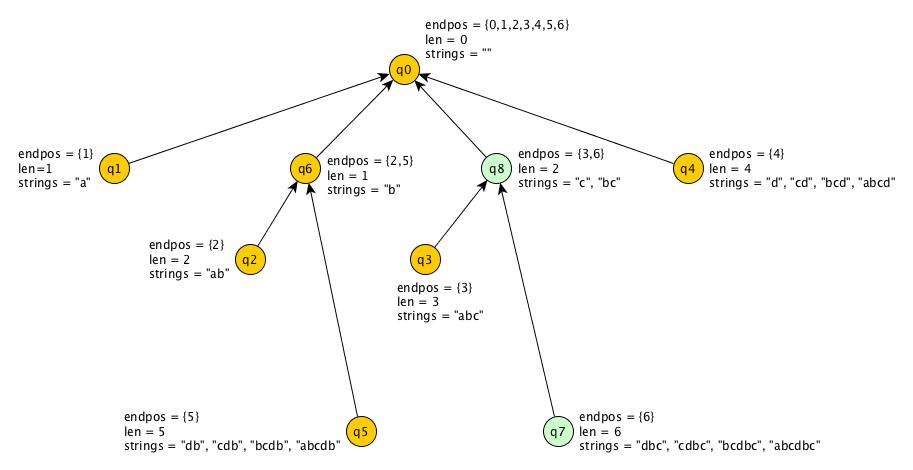Suffix Link Tree 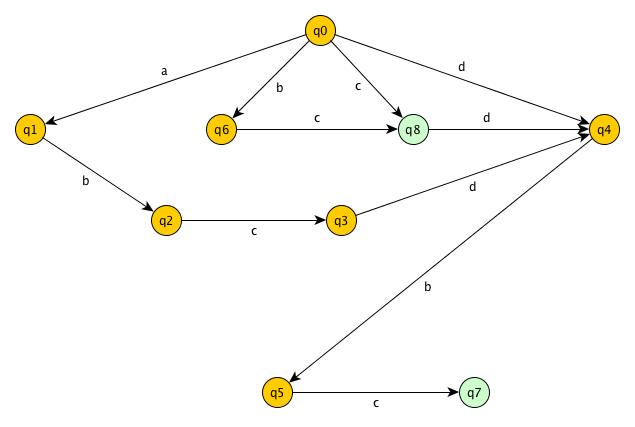Suffix Automata

Lemma 4: Let Q be a node, and let Q₁, Q₂, Q₃ … Qₙ be its children. That is, link(Q₁) = Q, link(Q₂) = Q, and so on. Then,

endpos(Q) ∪ endpos(Q₂) ... ∪ endpos(Qₙ) ⊂ endpos(Q)
endpos(Qᵢ) ∩ endpos(Qⱼ) = φ                            (i!=j)

From the definition of suffix links and lemma 2, we have endpos(Qᵢ) ⊂ endpos(Q) for all i. Thus, endpos(Q₁) ∪ endpos(Q₂) … ∪ endpos(Qₙ) ⊂ endpos(Q).

Let, endpos(Qᵢ) ∩ endpos(Qⱼ) != φ. Then, from Lemma 2, we know that one is contained in the other. Without loss of generality, let endpos(Qᵢ) ⊂ endpos(Qⱼ) (proper subset since i!=j). From the definition of suffix links, we know that endpos(Qᵢ) ⊂ endpos(link(Qᵢ)) ⊂ endpos(link(link(Qᵢ))) … and so on. Thus, Q_jmust be one of link(link…link(Qᵢ)). But, we have endpos(Qⱼ) ⊂ endpos(Q). Thus, endpos(Qⱼ) ⊂ endpos(link(Qᵢ)), which is a contradiction.

Observation 5: If we build a tree from the available sets of endpos-equivalence, such that the parent is a union of it’s (disjoint) children, it will be similar in structure to the suffix link tree, apart from the condition that it will instead follow the property,

endpos(Q₁) ∪ endpos(Q₂) ... ∪ endpos(Qₙ) = endpos(Q)

To see the difference, see the suffix link tree for S = “aba”.

Building Algorithm

The algorithm is online. We build the Suffix Automata incrementally, adding one character every time.

Some definitions:

Every state represents an equivalence class, which matches the substrings that belong to this equivalence class.
Let v be some state in the machine. Let longest(v) be the longest substring that matches at v, and let its length be len(v). Let the length of the shortest substring that matches at v be minlen(v). Then,
```
minlen(v) = len(link(v)) + 1
```
last points to the state that matches the entire string till this point (i.e., till the point the SA is built).

To ensure linearity in memory consumption, the data that we persist at every state is:

Length of the longest string that matches at this state: len
Suffix link: link
DFA-transitions: next

Initial State

The SA consists of a single state, q₀.

len(q₀) = 0
link(q₀) = nullptr
next(q₀) = { }
last = q₀

Adding a Character

Suppose we are adding character c to the Suffix Automata.

Create a new state, say cur. Set len(cur) = len(last) + 1.
Let iter_variable be last. Iterate till iter_variable has no transition on character c or iter_variable is nullptr:
- Add a transition on character c to cur in state iter_variable
```
  iter_variable.next(c) = cur
```
- Travel along the suffix link
```
  iter_variable = link(iter_variable)
```
If p == nullptr, assign link(cur) = q₀.
Else, let q be the state to which there is a transition at state p on seeing character c. (i.e., q = p.next(c))
If len(q) == len(p) + 1, assign link(cur) = q.
Else, make a copy of state q, say clone.
Set len(clone) = len(p) + 1. Set link(cur) = clone and link(q) = clone.
Let iter_variable be p. Iterate till iter_variable has a transition on character c or iter_variable is nullptr:
- Change the transition on character c to clone in state iter_variable.
```
  iter_variable.next(c) = clone
```
Set last to cur.

To mark the Accepting States of our DFA, after building the complete SA, we can start from last, and travel along the suffix links, marking all encountered states as Accepting. (Why?)

Proof of Correctness and Linearity

I’ll add the proofs in part-two of this blog post. I’m purposely not adding them here, to keep this part concise. I shall wait for some feedback, before I proceed with them.

Implementation

This is just a sample implementation. It can be optimised further for various purposes.

class SAutomata
{    private:
	class SNode
	{
		public:
			int link, len;
			map<char,int> next;
			SNode()
			{
				link = -1; 
				len = 0;
			}
			SNode(const SNode& other)
			{
				link = other.link;
				len = other.len;
				next = other.next;
			}
	};
	vector nodes;
	int last, cur;


    public:

	SAutomata(string S)
		: nodes(2*S.size()),
		dp(2*S.size(), -1),
		last(0),
		cur(1)
	{
		for(int i=0; i<S.size(); i++)
			add_char(S[i]);
	}
	void add_char(char A)
	{
		trace(A);
		int nw = cur++;
		nodes[nw].len = nodes[last].len+1;
		int p=last;
		for(; p!=-1 && nodes[p].next.find(A)==nodes[p].next.end(); p=nodes[p].link)
		{
			nodes[p].next[A]=nw;
		}
		if(p==-1)
		{
			nodes[nw].link = 0;
		}
		else if(nodes[nodes[p].next[A]].len == nodes[p].len + 1)
		{
			nodes[nw].link = nodes[p].next[A];
		}
		else
		{
			int nxt = nodes[p].next[A];
			int clone = cur++;
			nodes[clone] = nodes[nxt];
			nodes[clone].len = nodes[p].len + 1;
			nodes[nxt].link = clone;
			nodes[nw].link = clone;
			for(; p!=-1 && nodes[p].next.find(A)!=nodes[p].next.end() &&  nodes[p].next[A]==nxt; p=nodes[p].link)
			{
				nodes[p].next[A]=clone;
			}
		}
		last = nw;
	}};

Sample Problem

Let’s see a very basic problem.

Count the number of distinct substrings that occur in a given string.

You can solve this problem in two ways.

The number of different substrings is equal to the number of different possible paths we can take in the Suffix Automata. The number of distinct paths can be quite high ( O(n²) ), but we can use DP to save the number of paths possible from this state, and thus get the answer in O(n).
Using Suffix Links. Each node accepts substrings from minlen to len, i.e. len-minlen+1 substrings, and each of these is unique.

Try to get this problem accepted on SPOJ using both 1 and 2.

You can check my submission here. dfs() uses approach 1, while dfs2() uses approach 2.

Road Ahead

The part two of this blog post would be more focussed on questions and examples, the proof of correctness and linearity of the construction algorithm, converting the Suffix Automata to Suffix Tree and vice versa.

Till then, you can try out a few problems. For example, longest common substring in O(n); the count, total length, positions of occurence, and lexicographically k^th smallest of all distinct substrings in a given string, etc.

I look forward to some feedback, before I proceed with the second part.

References

← Top